A collision is an isolated event in which two or more moving bodies (colliding bodies) exert forces on each other for a relatively short time.
Although the most common colloquial use of the word "collision" refers to accidents in which two or more objects collide, the scientific use of the word "collision" implies nothing about the magnitude of the forces.
Some examples of physical interactions that scientists would consider collisions:
- An insect touches its antenna to the leaf of a plant. The antenna is said to collide with leaf.
- A cat walks delicately through the grass. Each contact that its paws make with the ground is a collision. Each brush of its fur against a blade of grass is a collision.
Collision is short duration interaction between two bodies or more than two bodies simultaneously causing change in motion of bodies involved due to internal forces acted between them during this. Collisions involve forces (there is a change in velocity). The magnitude of the velocity difference at impact is called the closing speed. All collisions conserve momentum. What distinguishes different types of collisions is whether they also conserve kinetic energy.Line of impact - It is the line which is common normal for surfaces are closest or in contact during impact. This is the line along which internal force of collision acts during impact and Newton's coefficient of restitution is defined only along this line.
Specifically, collisions can either be elastic, meaning they conserve both momentum and kinetic energy, or inelastic, meaning they conserve momentum but not kinetic energy. An inelastic collision is sometimes also called a plastic collision.
You are the maker of the program and which integrates data .... let's join here
A “perfectly-inelastic” collision (also called a "perfectly-plastic" collision) is a limiting case of inelastic collision in which the two bodies stick together after impact.
The degree to which a collision is elastic or inelastic is quantified by the coefficient of restitution, a value that generally ranges between zero and one. A perfectly elastic collision has a coefficient of restitution of one; a perfectly-inelastic collision has a coefficient of restitution of zero.
static var GRENADE_AMMO = 0;
function OnControllerColliderHit(hit : ControllerColliderHit){ if(hit.gameObject.tag == "crateGrenades"){ print("box of ammo Found"); //destroy the ammo box Destroy(hit.gameObject); //add ammo to inventory GRENADE_AMMO += 8;print("you now have "+ GRENADE_AMMO +"grenades");}}
var rayCastlength = 5 ;
function Update(){var hit : RaycastHit ;
// check if we're colliding if(Physics.Raycast(transform.position, transform.forward, hit, rayCastlength)){//with a door_openif(hit.collider.gameObject.tag == "door"){//open the door_openhit.collider.gameObject.animation.Play("door_open");}}}
Collisions play an important role in cue sports. Because the collisions between billiard balls are nearly elastic, and the balls roll on a surface that produces low rolling friction, their behavior is often used to illustrate Newton's laws of motion. After a zero-friction collision of a moving ball with a stationary one of equal mass, the angle between the directions of the two balls is 90 degrees. This is an important fact that professional billiards players take into account,[1] although it assumes the ball is moving frictionlessly across the table rather than rolling with friction. Consider an elastic collision in 2 dimensions of any 2 masses m1 and m2, with respective initial velocities u1 and u2 = 0, and final velocities V1 and V2. Conservation of momentum gives m1u1 = m1V1+ m2V2. Conservation of energy for an elastic collision gives (1/2)m1|u1|2 = (1/2)m1|V1|2 + (1/2)m2|V2|2. Now consider the case m1 = m2: we obtain u1=V1+V2 and |u1|2 = |V1|2+|V2|2. Taking the dot product of each side of the former equation with itself, |u1|2 = u1•u1 = |V1|2+|V2|2+2V1•V2. Comparing this with the latter equation gives V1•V2 = 0, so they are perpendicular unless V1 is the zero vector (which occurs if and only if the collision is head-on).
Let the linear, angular and internal momenta of a molecule be given by the set of r variables { pi }. The state of a molecule may then be described by the range δwi = δp1δp2δp3 ... δpr. There are many such ranges corresponding to different states; a specific state may be denoted by the index i. Two molecules undergoing a collision can thus be denoted by (i,j) (Such an ordered pair is sometimes known as a constellation.) It is convenient to suppose that two molecules exert a negligible effect on each other unless their centre of gravities approach within a critical distance b. A collision therefore begins when the respective centres of gravity arrive at this critical distance, and is completed when they again reach this critical distance on their way apart. Under this model, a collision is completely described by the matrix 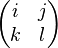 , which refers to the constellation (i, j) before the collision, and the (in general different) constellation (k, l) after the collision. This notation is convenient in proving Boltzmann's H-theorem of statistical mechanics.
, which refers to the constellation (i, j) before the collision, and the (in general different) constellation (k, l) after the collision. This notation is convenient in proving Boltzmann's H-theorem of statistical mechanics.
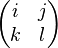 , which refers to the constellation (i, j) before the collision, and the (in general different) constellation (k, l) after the collision. This notation is convenient in proving Boltzmann's H-theorem of statistical mechanics.
, which refers to the constellation (i, j) before the collision, and the (in general different) constellation (k, l) after the collision. This notation is convenient in proving Boltzmann's H-theorem of statistical mechanics.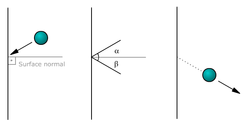

Tidak ada komentar:
Posting Komentar